series and parallel circuits
Components(R,L,C ) of an electrical circuit or electronic circuit can be connected in series, parallel or series-parallel. The two simplest of these are called series and parallel .
A circuit components connected in series is known as a series circuit . like this, one connected completely in parallel is known as a parallel circuit.
Current
In a series circuit, the current is the same for all of the elements.
Voltage
In a series circuit, the voltage is the sum of the voltage drops of the individual components (individual resistance ).
Individual Resistance
The total resistance of resistance [Rs] in series is equal to the sum of their individual resistances:
Rs= Resistance is in series
Electrical conductance presents a reciprocal quantity to resistance. Total conductance of a series circuits of pure resistances, can be calculated from the following formula:.In case of two resistances in series, the total conductance is equal to:
Inductors
In Inductors , the total inductance of non-coupled inductors in a series circuit is equal to the sum of their individual inductance's:

In many situations, it is difficult to prevent adjacent inductors from influencing each other, as the magnetic field of one device coupled with the winding's of its nearest one . This influence is defined as the mutual inductance M. For example if two inductors are in series, then there are two possible equivalent inductance's depending on how their magnetic fields of both inductors influence each other.When there are more than two inductors, the mutual inductance between each of them and the way the coils influence each other complex is the calculation. For a larger no. of coils the total combined inductance is given by the sum of all mutual inductance's between the various coils including the mutual inductance of each given coil with itself, which we called self-inductance or simple inductance.
For three coils, there are six mutual inductance's , , and , and . There are also the three self-inductance's of the three coils: , and .
HenceBy reciprocity = so that the last two groups can be combined. The first three terms represent the sum of the self-inductance's of the various coils. The formula is extended to any number of series coils with mutual coupling. The method can be used to find the self-inductance of large coils of wire of any cross-sectional shape by computing the sum of the mutual inductance of each turn of wire in the coil with every other turn since in such a coil all turns are in series.
Capacitors
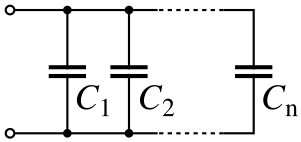
Capacitors similar to law using the reciprocals.The total capacitance of capacitors in series is equal to the reciprocal of the sum of the reciprocals of their individual capacitance's: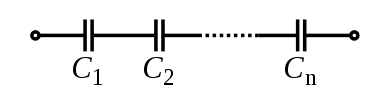
parallel circuits
If two or more components[R,L,C] are connected in parallel, they have the same difference of potential across their ends. The potential differences across the components are the same in magnitude, and they have identical polarities. The same voltage is applied to all circuit components which are connected in parallel. The total current is the sum of the currents through the individual components, according Kirchhoff’s current law.
Voltage
In a parallel circuit, the voltage is equal for all elements.
Current
The current in each individual resistor is calculated by Ohm's law. calculating voltage gives
.
Resistance
To calculate the total resistance of all components, add the reciprocals of the resistances of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:
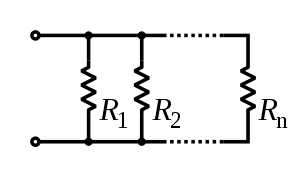
.For two resistances, the unreciprocated expression is
For N equal resistances in parallel, the reciprocal summation expression .and .To calculate the current in a component with resistance , use Ohm's law.The components divide the current according to their reciprocal resistances, in the case of two resistors,.An old term for devices connected in parallel is multiple, such as multiple connections for arc lamps.Hence, electrical conductance is reciprocal to resistance, the formula for total conductance of a parallel circuit of resistors is.The relations for total conductance and resistance stand in a complementary relationship: the expression for a series connection of resistances is the same as for parallel connection of conductance's and vice versa.
Inductors
The total inductance of non-coupled inductors in parallel is equal to the reciprocal of the sum of the reciprocals of their individual inductance's:

- .


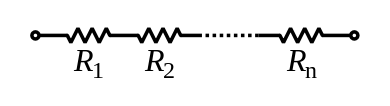







































No comments:
Post a Comment