Theorems:
Super Position Theorem:
Theorems:
Super Position Theorem:
Super Position Theorem that current through, or voltage across, any element of a network is equal to the algebraic sum of the currents or voltages produced independently by each source.
In other words, this theorem allows us to find a solution for a current or voltage using only one source at a time. Once we have the solution for each source, we can combine the results to obtain the total solution. The term algebraic appears in the above theorem statement because the currents resulting from the sources of the network can have different directions, just as the resulting voltages can have opposite polarities. If we are to consider the effects of each source, the other sources obviously must be removed. Setting a voltage source to zero volts is like placing a short circuit across its terminals. Therefore, when removing a voltage source from a network schematic, replace it with a direct connection (short circuit) of zero ohms. Any internal resistance associated with the source must remain in the network. Setting a current source to zero amperes is like replacing it with an open circuit. Hence, when removing a current source from a network schematic, replace it by an open circuit of infinite ohms. Any internal resistance associated with the source must remain in the network
Removing a voltage source and a current source to satisfy the superposition theorem.
Since the effect of each source will be determined independently, the number of networks to be analyzed will equal the number of sources.
If a particular current of a network is to be determined, the contribution to that current must be determined for each source. When the effect of each source has been determined, those currents in the same direction are added, and those having the opposite direction are subtracted; the algebraic sum is being determined. The total result is the direction of the larger sum and the magnitude of the difference. Similarly, if a particular voltage of a network is to be determined, the contribution to that voltage must be determined for each source. When the effect of each source has been determined, those voltages with the same polarity are added, and those with the opposite polarity are subtracted; the algebraic sum is being determined. The total result has the polarity of the larger sum and the magnitude of the difference.
Removing a voltage source and a current source to satisfy the superposition theorem.
Since the effect of each source will be determined independently, the number of networks to be analyzed will equal the number of sources.
If a particular current of a network is to be determined, the contribution to that current must be determined for each source. When the effect of each source has been determined, those currents in the same direction are added, and those having the opposite direction are subtracted; the algebraic sum is being determined. The total result is the direction of the larger sum and the magnitude of the difference. Similarly, if a particular voltage of a network is to be determined, the contribution to that voltage must be determined for each source. When the effect of each source has been determined, those voltages with the same polarity are added, and those with the opposite polarity are subtracted; the algebraic sum is being determined. The total result has the polarity of the larger sum and the magnitude of the difference.
Example:
calculate the current flowing through 20 Ω resistor of the following circuit using superposition theorem.
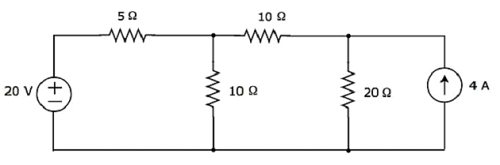Step 1 − Let us calculate the current flowing through 20 Ω resistor by considering only 20 V voltage source. In this case, we can eliminate the 4 A current source by making open circuit of it. The modified circuit diagram is shown below.
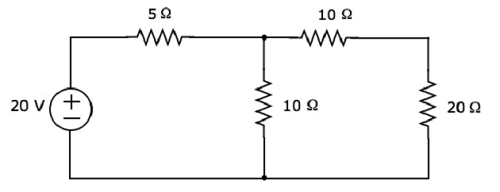There is only one principal node except Ground in the above circuit. So, we can use nodal analysis method. The node voltage V1 is labelled in the following figure. Here, V1 is the voltage from node 1 with respect to ground.
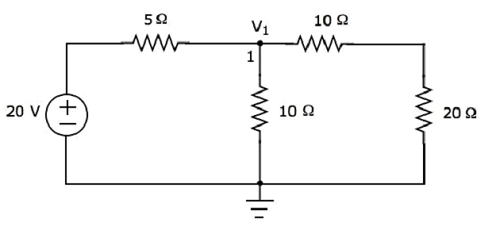The nodal equation at node 1 is
The current flowing through 20 Ω resistor can be found by doing the following simplification.
Substitute the value of V1 in the above equation.
Therefore, the current flowing through 20 Ω resistor is 0.4 A, when only 20 V voltage source is considered.
Step 2 − Let us find the current flowing through 20 Ω resistor by considering only 4 A current source. In this case, we can eliminate the 20 V voltage source by making short-circuit of it. The modified circuit diagram is shown in the following figure.
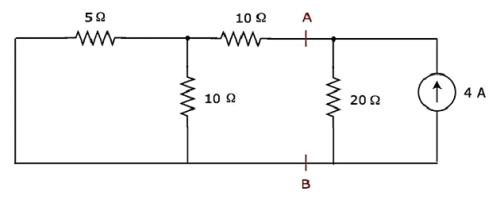In the above circuit, there are three resistors to the left of terminals A & B. We can replace these resistors with a single equivalent resistor. Here, 5 Ω & 10 Ω resistors are connected in parallel and the entire combination is in series with 10 Ω resistor.
The equivalent resistance to the left of terminals A & B will be
The simplified circuit diagram is shown in the following figure.
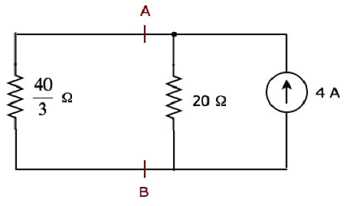We can find the current flowing through 20 Ω resistor, by using current division principle.
Substitute and in the above equation.
Therefore, the current flowing through 20 Ω resistor is 1.6 A, when only 4 A current source is considered.
Step 3 − We will get the current flowing through 20 Ω resistor of the given circuit by doing the addition of two currents that we got in step 1 and step 2. Mathematically, it can be written as
Substitute, the values of I1 and I2 in the above equation.
Therefore, the current flowing through 20 Ω resistor of given circuit is 2 A.
Note − We can’t apply superposition theorem directly in order to find the amount of power delivered to any resistor that is present in a linear circuit, just by doing the addition of powers delivered to that resistor due to each independent source. Rather, we can calculate either total current flowing through or voltage across that resistor by using superposition theorem and from that, we can calculate the amount of power delivered to that resistor using or .
Step 1 − Let us calculate the current flowing through 20 Ω resistor by considering only 20 V voltage source. In this case, we can eliminate the 4 A current source by making open circuit of it. The modified circuit diagram is shown below.
There is only one principal node except Ground in the above circuit. So, we can use nodal analysis method. The node voltage V1 is labelled in the following figure. Here, V1 is the voltage from node 1 with respect to ground.
The nodal equation at node 1 is
The current flowing through 20 Ω resistor can be found by doing the following simplification.
Substitute the value of V1 in the above equation.
Therefore, the current flowing through 20 Ω resistor is 0.4 A, when only 20 V voltage source is considered.
Step 2 − Let us find the current flowing through 20 Ω resistor by considering only 4 A current source. In this case, we can eliminate the 20 V voltage source by making short-circuit of it. The modified circuit diagram is shown in the following figure.
In the above circuit, there are three resistors to the left of terminals A & B. We can replace these resistors with a single equivalent resistor. Here, 5 Ω & 10 Ω resistors are connected in parallel and the entire combination is in series with 10 Ω resistor.
The equivalent resistance to the left of terminals A & B will be
The simplified circuit diagram is shown in the following figure.
We can find the current flowing through 20 Ω resistor, by using current division principle.
Substitute and in the above equation.
Therefore, the current flowing through 20 Ω resistor is 1.6 A, when only 4 A current source is considered.
Step 3 − We will get the current flowing through 20 Ω resistor of the given circuit by doing the addition of two currents that we got in step 1 and step 2. Mathematically, it can be written as
Substitute, the values of I1 and I2 in the above equation.
Therefore, the current flowing through 20 Ω resistor of given circuit is 2 A.
Note − We can’t apply superposition theorem directly in order to find the amount of power delivered to any resistor that is present in a linear circuit, just by doing the addition of powers delivered to that resistor due to each independent source. Rather, we can calculate either total current flowing through or voltage across that resistor by using superposition theorem and from that, we can calculate the amount of power delivered to that resistor using or .
No comments:
Post a Comment